Traces in voxel space
My current project required a method to trace a ray though a voxel space. This is a problem I figured would be pretty much solved and could just copy paste a solution into my codebase and carry on with other issues. Unfortunately not. While there are some source programs that purport to trace a voxel space they are set up for the nuances of that type of voxel and so weren’t immediately amenable to my problem. Furthermore they didn’t really have much of a description of how they were working. So I sat down and worked out how to do it! I’m writing it down here for three reasons: 1) It’s an excuse to blog :) 2) So people smarter than me can point out if anything is wrong (I hope nothing is) 3) So others can use and learn from it
I’m going to explain most of this in a 2D space, but the extension to 3D is trivial and I’ll show it at the end.
Problem:
Given two spaces, a world space (which I’ll measure in millimetres “mm”) and a grid/voxel space (1 voxel = 100 mm) we want to trace a line between two points in world space and get back which voxels are intersected by this line. That is a function (point start, point end) -> list
Step one is to find which voxel our end points are currently in.
Voxel p0 = start / 100
Voxel p1 = end / 100If your space can be negative you need to make sure you do the correct division here! -50 / 100 should be -1 not 0. See Euclidean division
Next is to calculate a direction vector between the start and end points
Vector dir = end - startThis can be understood as a velocity vector, it’s units are mm/t where t is our arbitrary time unit. This means we travel from start to end in 1t.
Given the direction we call sign (returns -1,0 or 1) on the two direction components. This will be used to step our voxel indices later.
int dx = Sign(dir.x)
int dy = Sign(dir.y)Now we calculate the delta in time space per voxel. That’s a bit of a mouth full so lets take it step by step. First we know that dir is mm/t and that 100mm equals 1 voxel, so if dv=dir/100 then dv is measured in voxel/t. That is how many voxels we move in 1 time unit. If then take the reciprocal of that (dt=1/dv) then dt is measured in t/voxel, or in other words how many time units it takes to move 1 voxel. Bit of rearrangement gives:
float dtx = 100.0 / Abs(dir.x)
float dty = 100.0 / Abs(dir.y)While dir could be an integer vector if you world points were integers the calculation here needs to be done with floats.
Moving on we calculate the extents of the starting voxel in world space. This is simply multiplying its index by 100 for the minimum extent and then adding 100 to that for the maximum extent.
Point min = p0 * 100
Point max = min + 100Now given this box and the direction we’re tracing (remember dx/dy) we find the distance in each axis from the start point to the next axis plane between voxels. So if start.x is at 570mm and we are moving positively then the distance to the next plane is 600mm - 570mm or 40mm. Same for y.
int distx = dx >= 0 ? (max.x - start.x) : (start.x - min.x)
int disty = dy >= 0 ? (max.y - start.y) : (start.y - min.y)If moving positively (or not all, doesn’t really matter in that case), the return the distance between start and the max extents else return the distance between start and the min extents.
Those distances are in mm we need them in voxels so a quick division by hundred later.
float distvx = distx / 100
float distvy = disty / 100Again note we need floats here.
Finally the last step of initialisation. Given the distance in voxels to the next voxel in each axis and the time units per voxel again in each axis we work out how far away we are in time space from the next voxel!
float tx = distvx * dtx
float ty = distvy * dtytx and ty tell us at what time we cross over into the next voxel in that direction. Given all this information we can loop until we get to the end.
int x = p0.x
int y = p0.y
while (true)
{
yield Voxel(x, y)
if (tx <= ty)
{
if (x == p1.x) break;
tx += dtx;
x += dx;
}
else
{
if (y == p1.y) break;
ty += dty;
y += dy;
}
}On each iteration of the loop we yield the current voxel (so we will always yield the start voxel). We then check if tx is less than ty, if it is we know we’ve hit the x axis boundary between two voxels. If it’s the last voxel we break out the loop otherwise we add dtx (which tells us how far in t till the next x axis boundary) to tx and add dx (+/-1) to our current voxel. Likewise if ty is less than tx we do the same but in the y axis.
Hopefully that’s a good enough description. If you spot anything wrong please point it out. I’ll leave you with two final things, first the above algorithm for 3D, and second a program for SlimDX.Direct2D to experiment tracing grids.
Voxel p0 = start / 100
Voxel p1 = end / 100
Vector dir = end - start
int dx = Sign(dir.x)
int dy = Sign(dir.y)
int dz = Sign(dir.z)
float dtx = 100.0 / Abs(dir.x)
float dty = 100.0 / Abs(dir.y)
float dtz = 100.0 / Abs(dir.z)
Point min = p0 * 100
Point max = min + 100
int distx = dx >= 0 ? (max.x - start.x) : (start.x - min.x)
int disty = dy >= 0 ? (max.y - start.y) : (start.y - min.y)
int distz = dz >= 0 ? (max.z - start.z) : (start.z - min.z)
float distvx = distx / 100
float distvy = disty / 100
float distvz = distz / 100
double tx = distvx * dtx
double ty = distvy * dty
double tz = distvy * dtz
int x = p0.x
int y = p0.y
int y = p0.z
while (true)
{
yield Voxel(x, y, z)
if (tx <= ty && tx <= tz)
{
if (x == p1.x) break;
tx += dtx;
x += dx;
}
else if (ty <= tz)
{
if (y == p1.y) break;
ty += dty;
y += dy;
}
else
{
if (z == p1.z) break;
tz += dtz;
z += dz;
}
}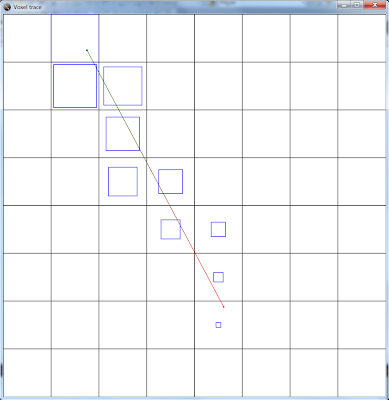
Green is the start point, red the end point. They are set by left and right click respectively. The blue squares indicate which grid points are hit by the ray getting smaller as they progress.
using System;
using System.Collections.Generic;
using System.Drawing;
using System.Linq;
using SlimDX.Direct2D;
using SlimDX.Windows;
namespace VoxelTrace
{
class Form : RenderForm
{
public Form()
{
ClientSize = new System.Drawing.Size(100 * Program.Lines, 100 * Program.Lines);
MaximumSize = MinimumSize = Size;
Text = "Voxel trace";
}
}
class Program
{
static Factory Factory;
static WindowRenderTarget RenderTarget;
static SolidColorBrush BlackBrush;
static SolidColorBrush BlueBrush;
static SolidColorBrush GreenBrush;
static SolidColorBrush RedBrush;
static LinearGradientBrush GreenRedBrush;
static Point P1, P2;
public const int Lines = 8;
static void Main(string[] args)
{
Form form = new Form();
Factory = new Factory();
var renderTargetProperties = new WindowRenderTargetProperties()
{
Handle = form.Handle,
PresentOptions = PresentOptions.Immediately,
PixelSize = form.ClientSize,
};
RenderTarget = new WindowRenderTarget(Factory, renderTargetProperties);
BlackBrush = new SolidColorBrush(RenderTarget, Color.Black);
BlueBrush = new SolidColorBrush(RenderTarget, Color.Blue);
GreenBrush = new SolidColorBrush(RenderTarget, Color.Green);
RedBrush = new SolidColorBrush(RenderTarget, Color.Red);
var gradientStops = new GradientStopCollection(RenderTarget, new GradientStop[] {
new GradientStop() { Color = Color.Green, Position = 0 },
new GradientStop() { Color = Color.Red, Position = 1 }});
var linearGradientBrushProperties = new LinearGradientBrushProperties()
{
StartPoint = P1, EndPoint = P2,
};
GreenRedBrush = new LinearGradientBrush(RenderTarget, gradientStops, linearGradientBrushProperties);
form.MouseClick += new System.Windows.Forms.MouseEventHandler(MouseClick);
MessagePump.Run(form, Tick);
}
static void MouseClick(object sender, System.Windows.Forms.MouseEventArgs e)
{
int x = e.X;
int y = e.Y;
if (e.Button == System.Windows.Forms.MouseButtons.Left)
P1 = new Point(x, y);
if (e.Button == System.Windows.Forms.MouseButtons.Right)
P2 = new Point(x, y);
GreenRedBrush.StartPoint = P1;
GreenRedBrush.EndPoint = P2;
Trace = Raytrace(P1, P2).ToArray();
}
static Point[] Trace;
static IEnumerable<Point> Raytrace(Point start, Point end)
{
int x0 = start.X / 100;
int y0 = start.Y / 100;
int x1 = end.X / 100;
int y1 = end.Y / 100;
SlimDX.Vector2 dir = new SlimDX.Vector2(end.X - start.X, end.Y - start.Y);
int dx = Math.Sign(dir.X);
int dy = Math.Sign(dir.Y);
double deltax = 100.0 / Math.Abs(dir.X);
double deltay = 100.0 / Math.Abs(dir.Y);
long minx = x0 * 100, maxx = minx + 100;
long miny = y0 * 100, maxy = miny + 100;
double distx = ((dx >= 0) ? (maxx - start.X) : (start.X - minx)) / 100.0;
double disty = ((dy >= 0) ? (maxy - start.Y) : (start.Y - miny)) / 100.0;
double tx = distx * deltax;
double ty = disty * deltay;
var prev = new Point(x0, y0);
while (true)
{
var grid = new Point(x0, y0);
yield return grid;
prev = grid;
if (tx <= ty)
{
if (x0 == x1) break;
tx += deltax;
x0 += dx;
}
else
{
if (y0 == y1) break;
ty += deltay;
y0 += dy;
}
}
}
public static void Tick()
{
RenderTarget.BeginDraw();
RenderTarget.Clear(Color.White);
for (int i = 0; i < Lines; ++i)
{
PointF x0 = new PointF(100 * i, 0), x1 = new PointF(100 * i, 100 * Lines);
PointF y0 = new PointF(0, 100 * i), y1 = new PointF(100 * Lines, 100 * i);
RenderTarget.DrawLine(BlackBrush, x0, x1);
RenderTarget.DrawLine(BlackBrush, y0, y1);
}
float radius = 2;
RenderTarget.FillEllipse(GreenBrush, new Ellipse() { Center = P1, RadiusX = radius, RadiusY = radius });
RenderTarget.FillEllipse(RedBrush, new Ellipse() { Center = P2, RadiusX = radius, RadiusY = radius });
RenderTarget.DrawLine(GreenRedBrush, P1, P2);
if (Trace != null)
{
for (int i = 0; i < Trace.Length; ++i)
{
Point p = Trace[i];
float size = (Trace.Length - i) * 100.0f / Trace.Length;
float offset = (100 - size) / 2;
var rect = new RectangleF(p.X * 100 + offset, p.Y * 100 + offset, size, size);
RenderTarget.DrawRectangle(BlueBrush, rect);
}
}
RenderTarget.EndDraw();
}
}
}